Welcome to Understanding CRDTs, a series of articles in which we’ll discuss CRDTs from the ground up. We’ll start from the basic concepts, trying to discuss different algorithms and data structures using simple JavaScript implementations, and we’ll gradually work towards a high-performance, JSON CRDT implementation written in Rust.

Chapters (so far):

1. A Gentle Introduction
2. Improving our Set

In the past two months, I’ve been diving deeper into the realm of distributed systems. The catalyst that started my research was discovering the world of local-first applications, a class of software that allows users to access and modify their data locally, while seamlessly synchronizing across devices, even in the face of connection failures.

From the lens of distributed system theory, local-first applications could be defined as multi-master, eventually-consistent, distributed databases. A replica of the database would run on every user’s device, allowing writes at all times and, when a connection with another replica is available, synchronize the changes. Moreover, depending on the specific algorithm chosen to implement this distributed database, we could relax many of the topology constraints of traditional systems: imagine a system that could seamlessly synchronize across user devices (eg. P2P), while also optionally synchronizing with a central server.

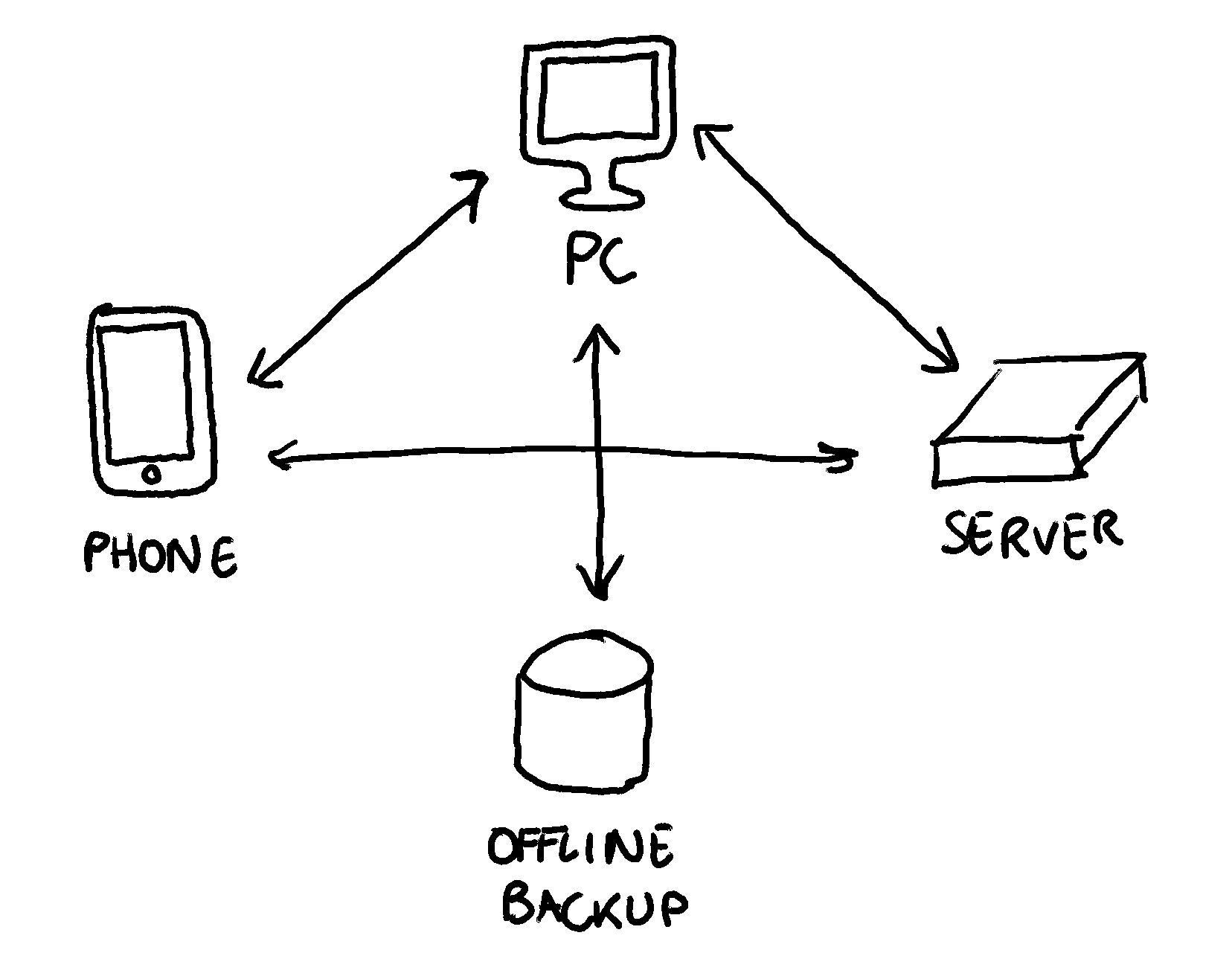
This architecture allows applications to offer a superb UX, allowing users to work even without an internet connection (eg. when flying on a plane or in the subway), without sacrificing the convenience of synchronization across devices, something that we take for granted nowadays. But if the UX is so much better for the end user, why do so many apps fail to implement such a model? For example, Notion, a very popular knowledge-base app, can’t work without an internet connection, leading to poor user experience in low-connectivity scenarios.

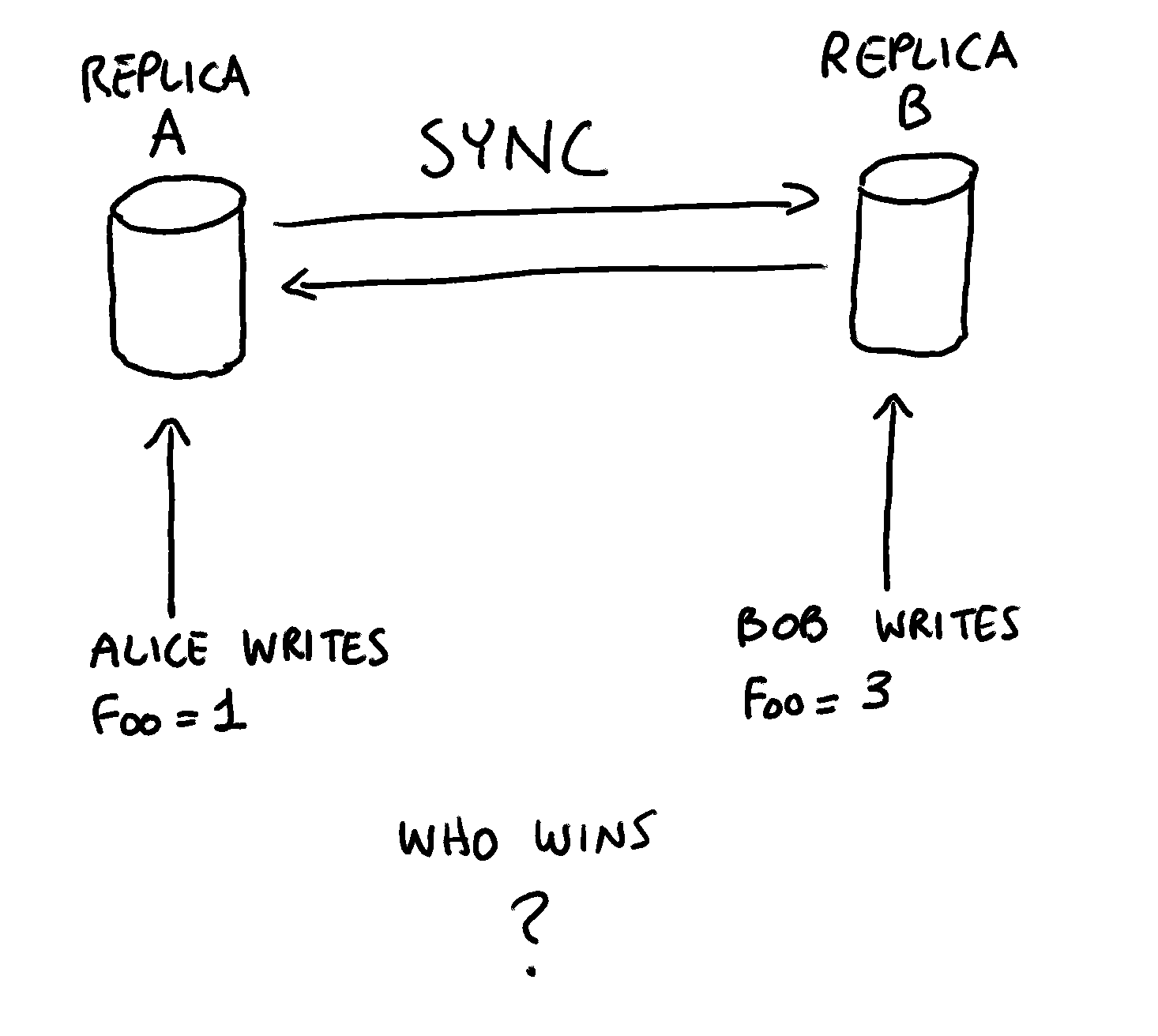
The answer is that implementing a robust multi-master replication is not trivial, and introduces several challenges. For example, what happens when two users write to the same entry concurrently?

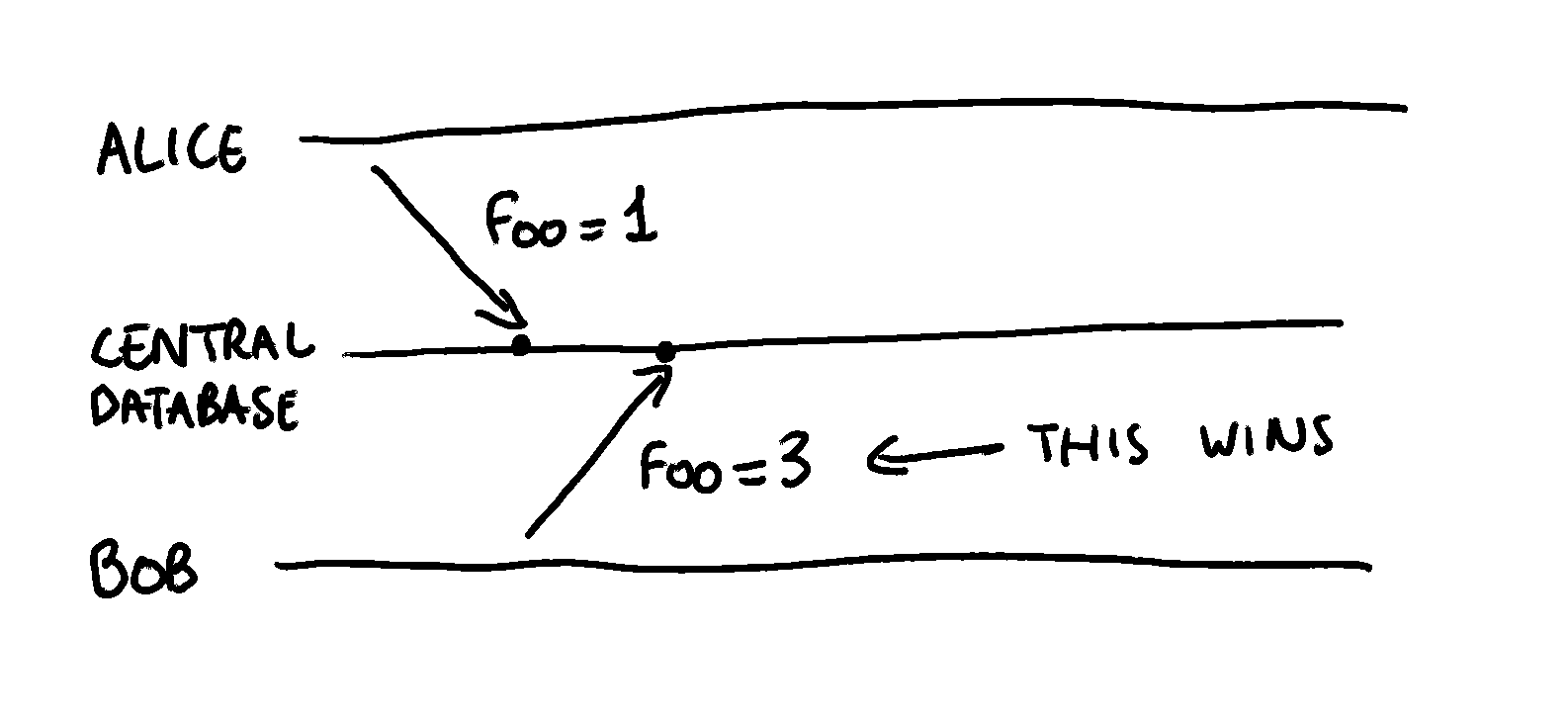
A traditional centralized database does not suffer from this problem, as all writes are handled by a single entity, which can decide with no ambiguity which update should take precedence.

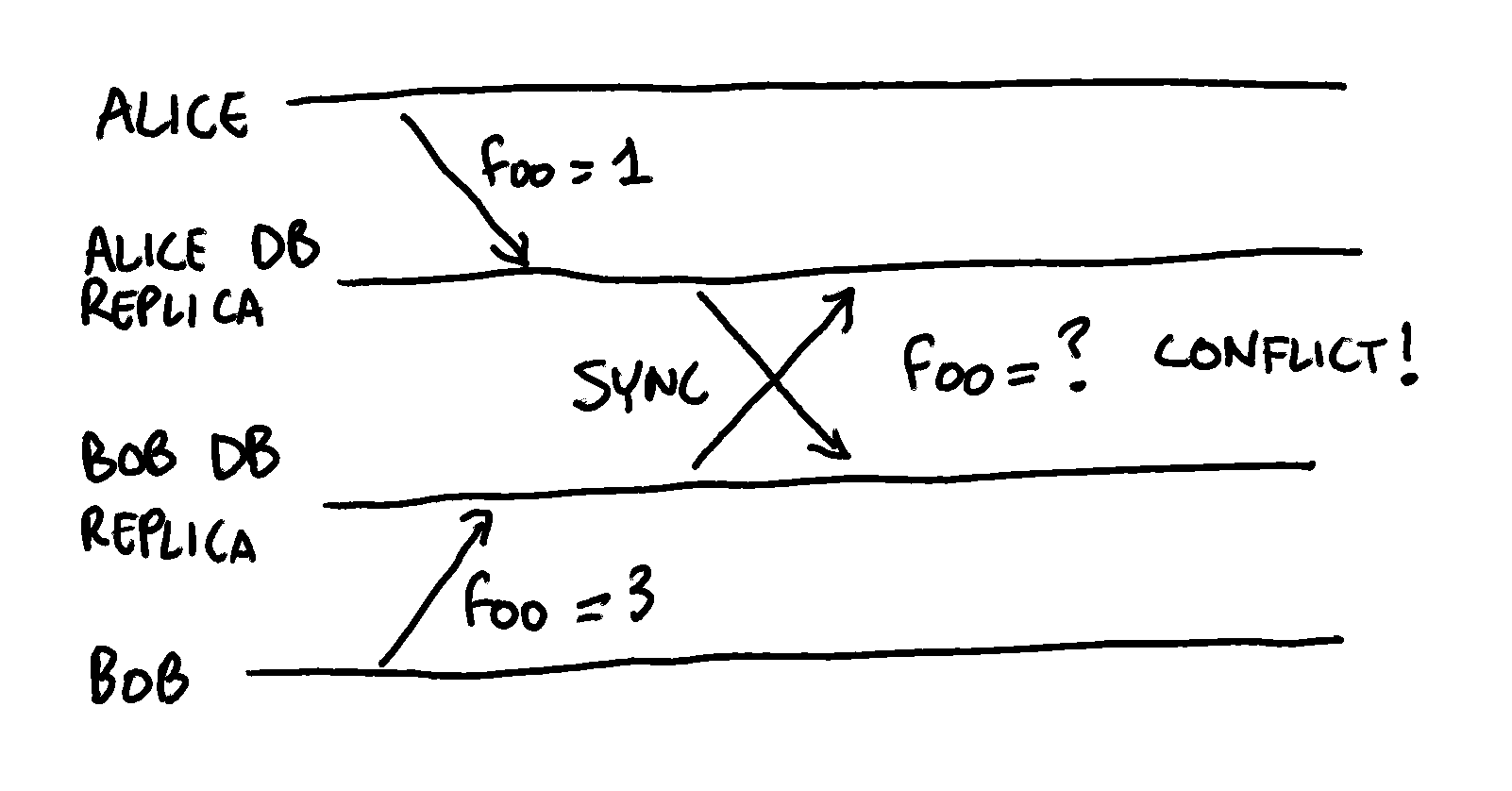
But in a multi-master architecture, all replicas typically have the same priority, so how do we decide which update “win”?

A first approach could be to have the last update take precedence, a concept known as Last Write Wins (LWW): in this scenario, the last update being performed overwrites the previous one. So theoretically, we could just attach to each update a timestamp, and the update with the highest timestamp wins. Sounds easy, right?

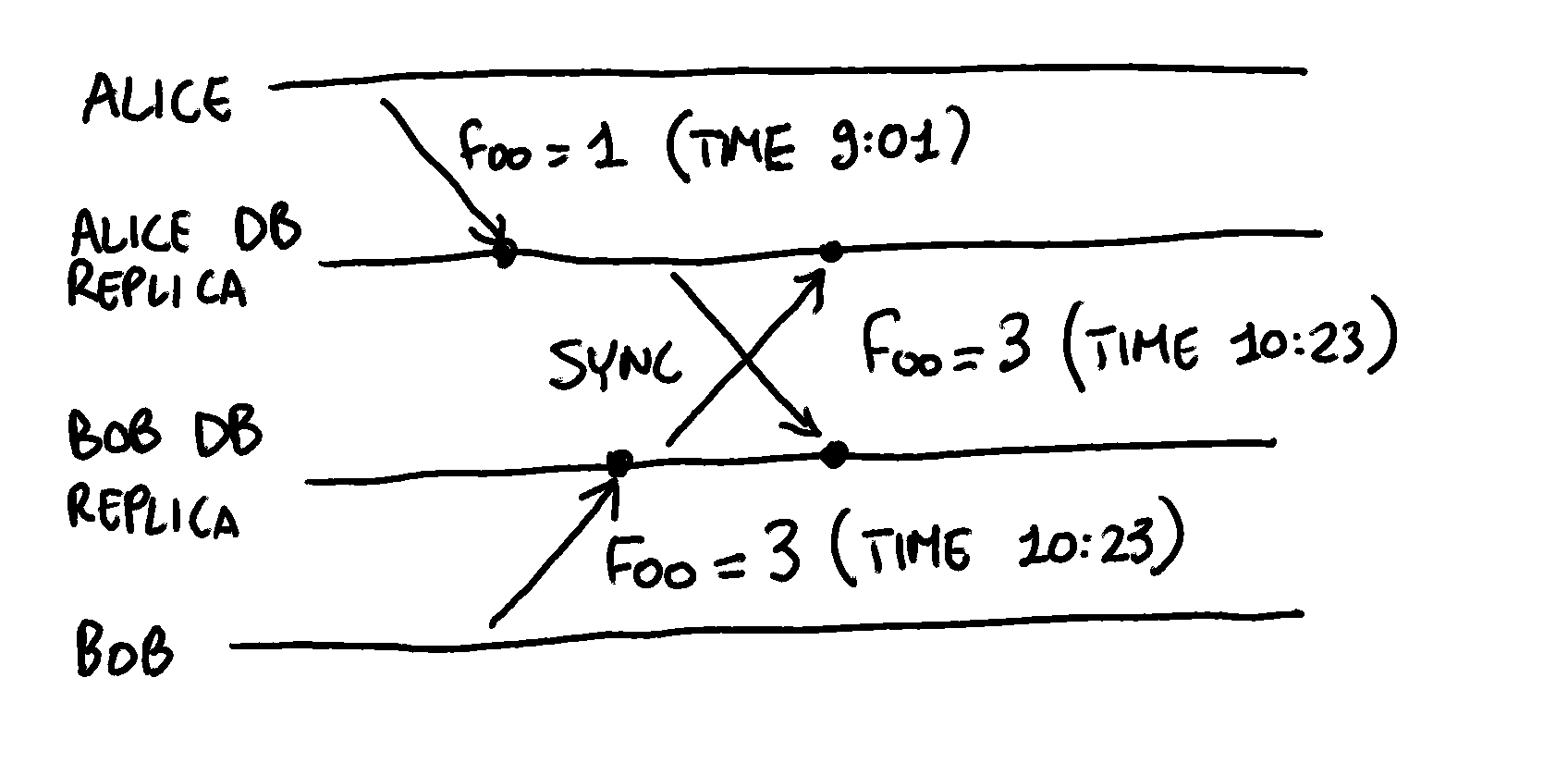
Well, we have a problem, in fact, a serious problem: in a distributed system, clocks are never perfectly in sync. They can drift forward, backward, and even be completely off. And while most operating systems will try their best to keep clocks in sync, it’s not something we should rely on to guarantee correctness or integrity. Would you trust a database that 99.99% of the time works perfectly, but silently corrupts the data if the clock goes off?

And it gets worse, because even if clocks are perfectly in sync, the LWW semantic isn’t always appropriate. Imagine the scenario of a distributed counter: what happens if two replicas increment the counter concurrently? If we adopt the LWW semantic, one of the two increments is going to be lost.

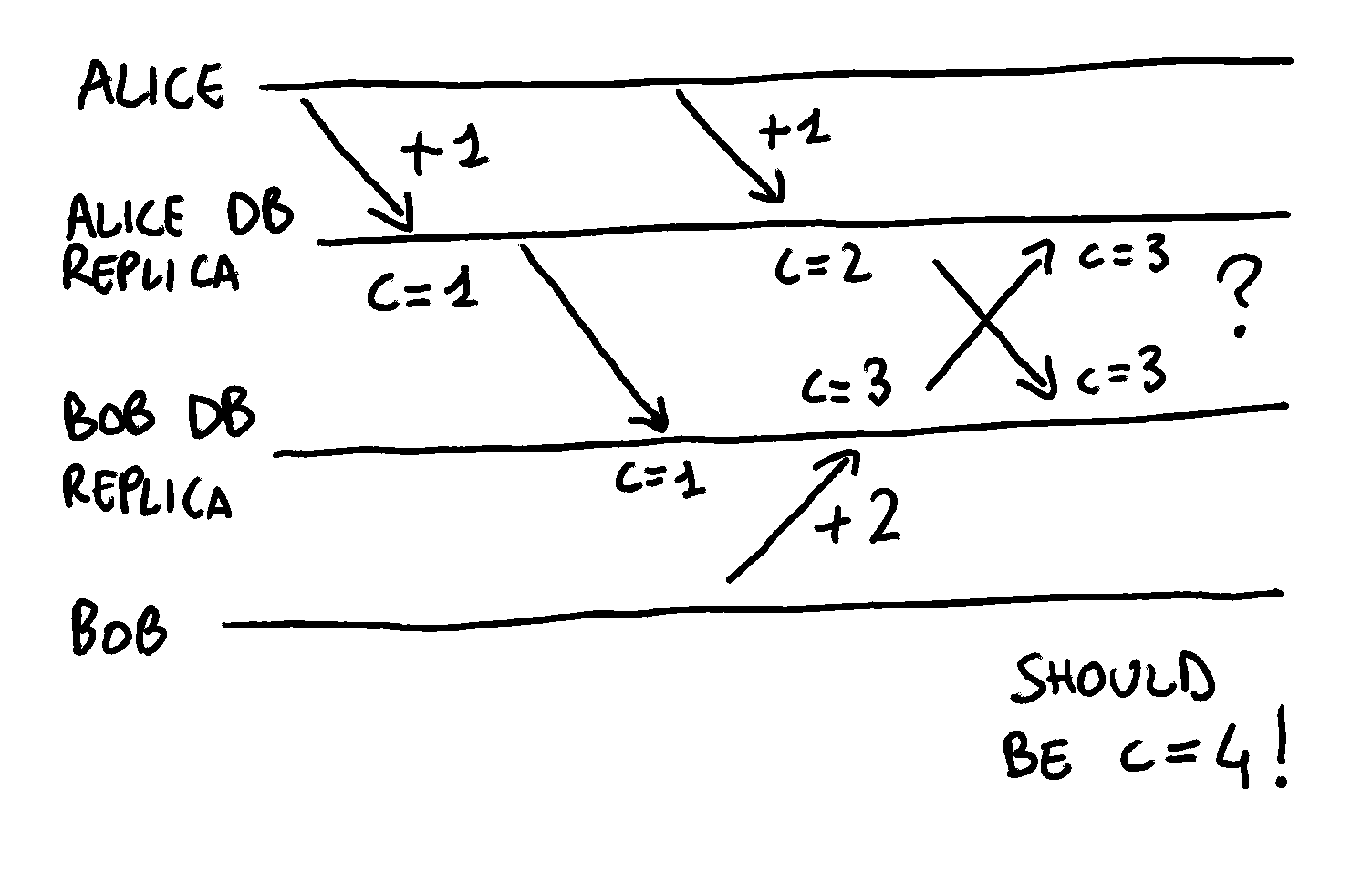
It turns out that different use cases and data structures require different approaches to deal with conflicts. As you can imagine, this could get complex pretty quickly. Luckily for us, distributed system theory comes to the rescue with the concept of CRDT.

Introducing CRDTs

Conflict-free Replicated Data Types, or CRDTs for short, are a class of data structures that can be replicated across nodes in a network, with the following features (quoting Wikipedia):

1. The application can update any replica independently, concurrently, and without coordinating with other replicas.
2. An algorithm (itself part of the data type) automatically resolves any inconsistencies that might occur.
3. Although replicas may have different state at any particular point in time, they are guaranteed to eventually converge.

In other words, nodes can always access and modify their local copy of the CRDT as if it was a plain data structure (eg. a HashMap), and the CRDT algorithm takes care of conflict resolution and eventual convergence. It’s important to keep in mind that CRDTs do not require consensus to operate: generally, there is no distinction between replicas in a CRDT, which contrasts with typical replicated databases, in which a particular node acts as a master, and others as read-only replicas.

The term data structure we used previously is purposefully generic: depending on the chosen approach, CRDTs can model widely different types of data structures: maps, lists, strings, trees, etc. So if you need a distributed data structure with the semantics of a HashMap, you can use a CRDT-based HashMap, and if you need to implement real-time text editing (eg. Google Docs) you can use a CRDT-based List of characters. Moreover, CRDTs can be composed nicely, so if you have a CRDT Map and a CRDT List, you can compose them to represent a JSON-like CRDT data structure, with nested objects and values.

Before diving into our first CRDT, it’s important to discuss the concept of intent preservation. We defined CRDTs as data structures that automatically resolve conflicts and eventually converge to the same value across replicas, but that’s only part of the picture. For example, we could think of a HashMap that never stores any value that is given to it:

class NoopMap {
  set(key, value) {
    // DO NOTHING
  }
  
  get(key) {
        return undefined;
  }
}

As crazy as it sounds, this data structure is a perfectly valid CRDT:

• Conflicts are automatically handled because no conflict can ever occur if we don’t store values
• Every replica always converges to the same value, an empty map

As you can imagine, despite being formally definable as a CRDT, this data structure is of little practical use. The reason is that in order for a CRDT algorithm to be good for practical purposes, it should try as much as possible to resolve conflicts while preserving the user’s intent, which has several important implications in our conflict resolution choices. We are going to cover this topic more in the following sections and chapters.

Our first CRDT: Set

Our CRDT adventure will start with a simple, yet very useful data structure: the Set.

First step: Add-only Set

To make our lives easier, we’ll narrow down our goal at first by creating an Add-only Set, that is, a set to which we can add elements but not remove them (this is an important aspect, more on this later).

Our goal is to create a CRDT with the semantics of an Add-only Set. In simple terms, we want a data structure with these features:

• Elements can be added to the structure (add operation)
• We can check if an element is present in the structure (has operation)
• Elements are not ordered (Set semantics)
• No duplicates (Set semantics)

For these examples, we will use JavaScript as it’s popular enough to be understood by most people (although some might argue that no one really understands JavaScript /s).

Let’s start by implementing our CRDTSet class:

class CRDTAddOnlySet {
    constructor() {
        this.set = new Set();
    }

    add(element) {
        this.set.add(element);
    }

    has(element) {
        return this.set.has(element);
    }
}

const set = new CRDTAddOnlySet();

set.add('a');
console.log(set.has('a')); // true
console.log(set.has('b')); // false

set.add('b');
console.log(set.has('b')); // true

Pretty straightforward so far: we created a CRDTSet class that wraps a Set and exposes the add and has operations.

Things start to get interesting when we introduce CRDT semantics, which we are going to cover in the next section.

Adding CRDT semantics

Our CRDTAddOnlySet currently lacks one of the most important features of a CRDT: convergence. In particular, we want every replica of our data structure to eventually converge to the same value.

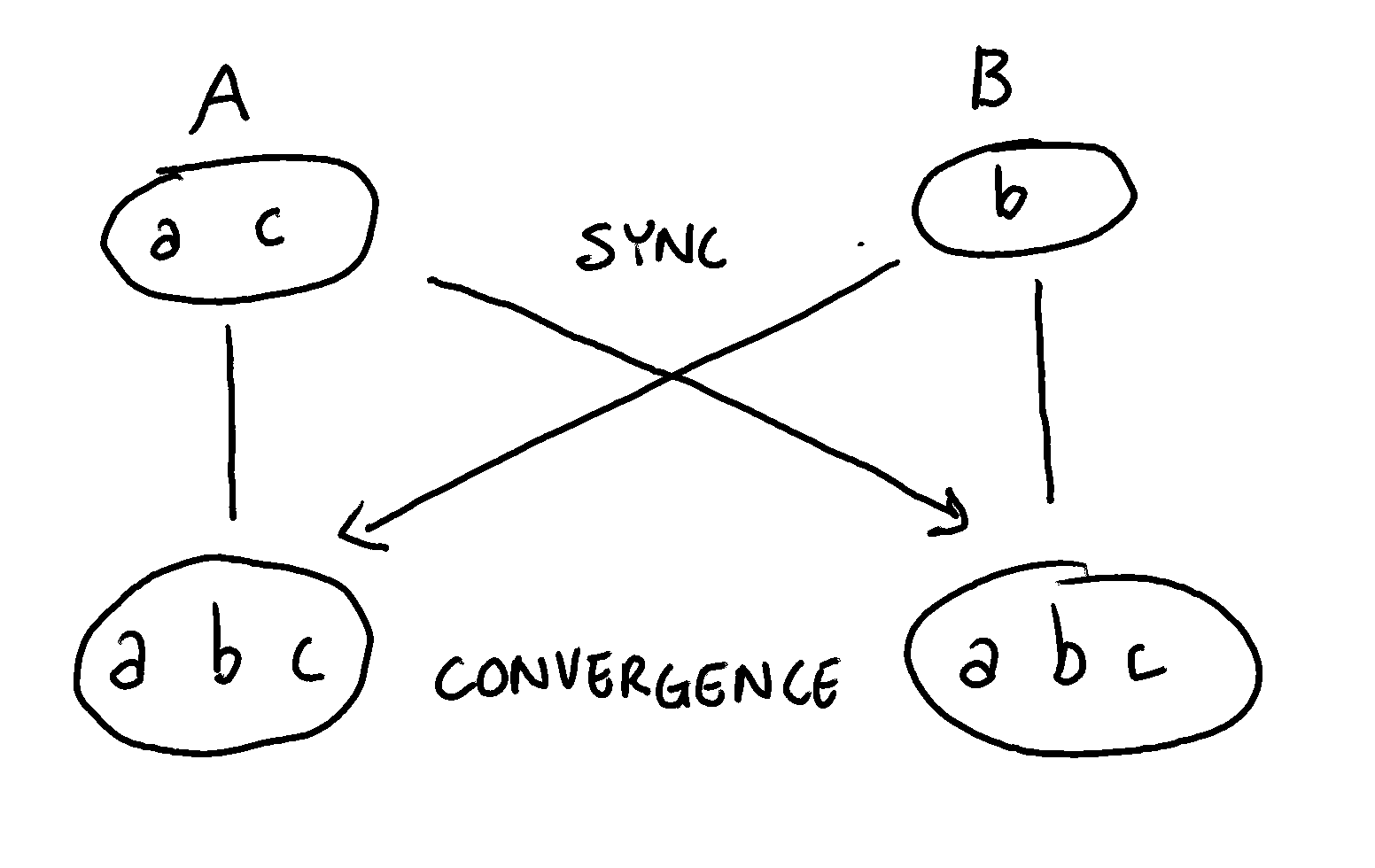
At this point, we are not interested in the specific protocol used by different replicas to send each others’ changes. Let’s just assume that each replica will periodically send its CRDTAddOnlySet value to the other replicas.

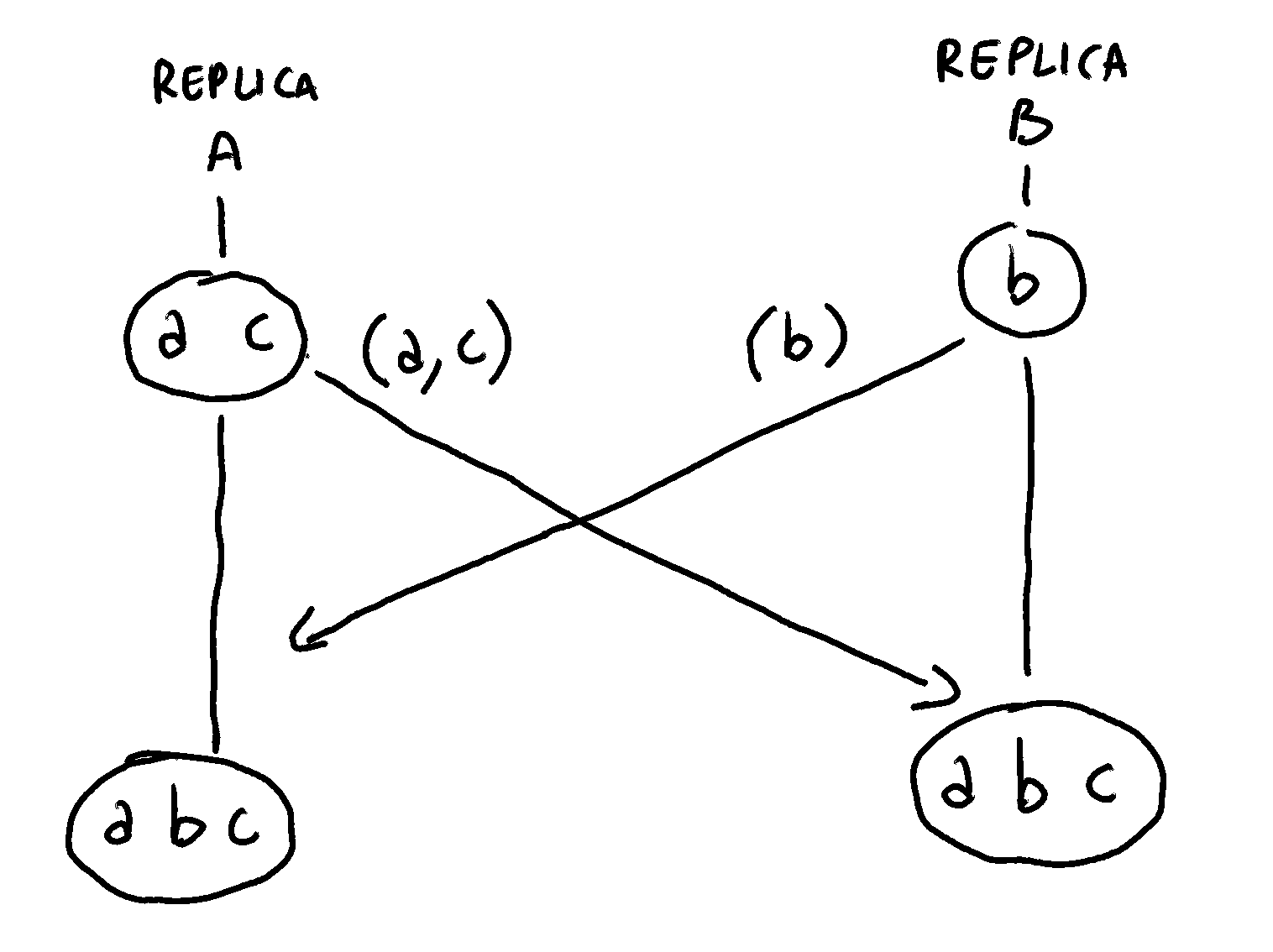
To handle the merging process, we’ll add a new method to our CRDTSet structure: merge. This method takes another CRDTAddOnlySet and merges all its elements with the current set:

merge(otherSet) {
    for (let element of otherSet.set) {
        this.set.add(element);
    }
}

With the merge method, we can now propagate changes among replicas. In this example, we propagate changes from replica B to replica A:

const replicaA = new CRDTAddOnlySet();
replicaA.add('a');
console.log(replicaA.has('a')); // true
console.log(replicaA.has('b')); // false

const replicaB = new CRDTAddOnlySet();
replicaB.add('b');
console.log(replicaB.has('a')); // false
console.log(replicaB.has('b')); // true

// Here we propagate the changes from replica B to replica A
replicaA.merge(replicaB);
console.log(replicaA.has('a')); // true
console.log(replicaA.has('b')); // true

Despite its simplicity, this approach offers some surprising advantages over traditional synchronization techniques:

• It’s highly decentralized: the algorithm imposes no constraint over the topology and communication between replicas. In particular, because the merging process is commutative and transitive, if replica A synchronizes with replica B, and then replica B synchronizes with replica C, then replica A and C will be in sync (as long as no concurrent update in A has happened in the meantime), despite having never communicated directly with each other.
• As a result, the system is extremely robust against network problems and downtimes, as it can transparently make use of a mesh network rather than a traditional centralized solution.

As you can imagine, there are downsides as well, which we’ll gradually cover in the following sections.

Adding support for Removals: a Naive Αttempt

Although an Add-only Set could be useful in some cases, many scenarios would also require removal operations, so our next goal is to add support for them. In short, we want to introduce a remove method that replicas can use to remove an element from the Set.

A first attempt could look as follows:

remove(element) {
    this.set.delete(element);
}

And if we try to run it:

const set = new CRDTSet();
set.add('a');
console.log(set.has('a')); // true
set.remove('a');
console.log(set.has('a')); // false

It works! Wait… does it? Apparently, the remove operation works correctly, but what happens when we synchronize the set across multiple replicas?

const replicaA = new CRDTSet();
replicaA.add('a');
console.log(replicaA.has('a')); // true

const replicaB = new CRDTSet();
replicaB.merge(replicaA);       // Sync replica B with replica A

replicaA.remove('a');
console.log(replicaA.has('a')); // false

replicaA.merge(replicaB);       // Sync replica A with replica B
console.log(replicaA.has('a')); // true!!! The 'a' came back!

We have a problem: although replica A deleted element a, synchronizing with replica B causes the a element to come back!

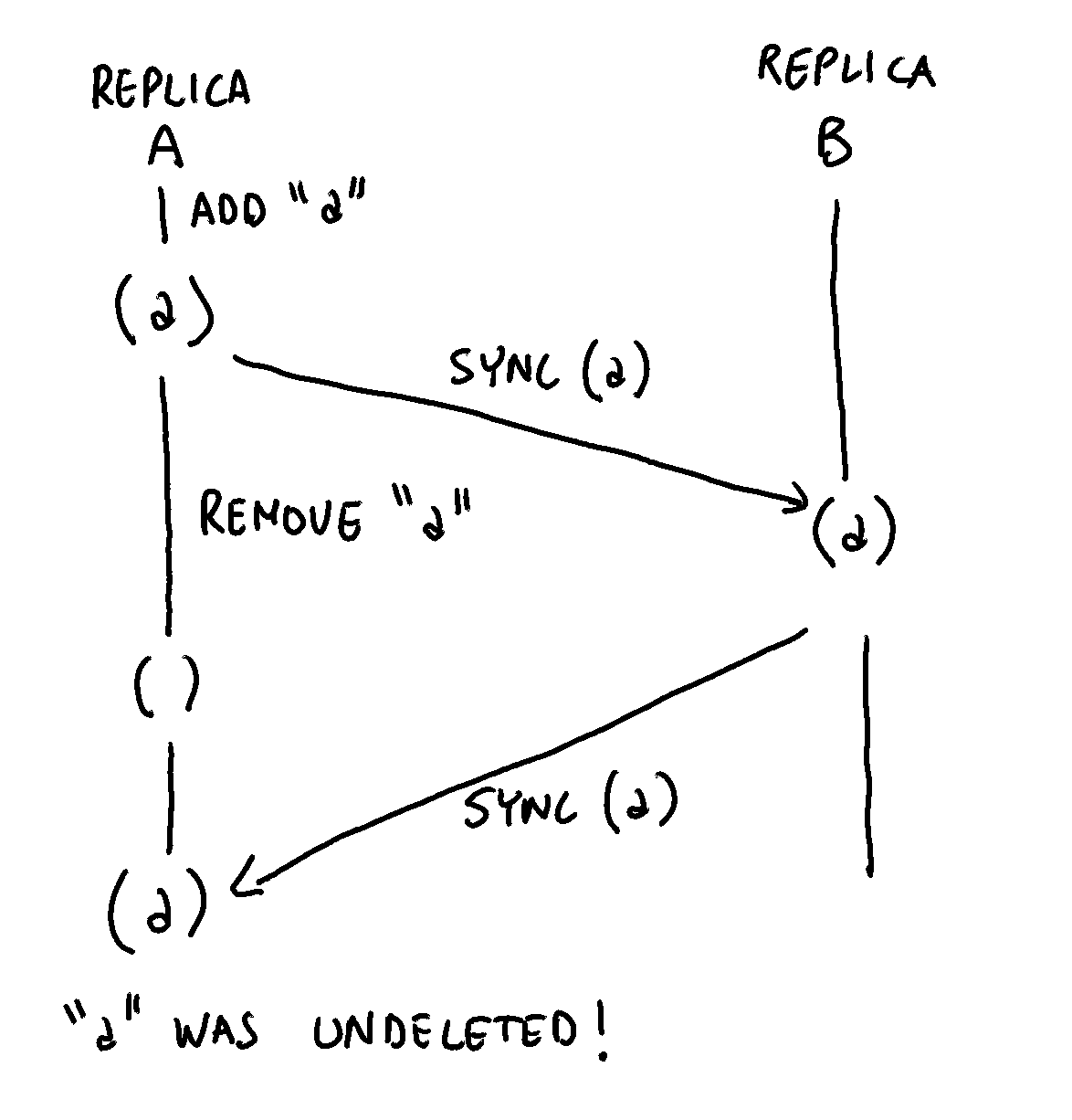
Our remove operation is quite flaky: depending on the synchronization sequence, elements can be randomly undeleted. How can we solve this problem?

Turns out that delete operations are one of the core complexities of CRDTs, and multiple approaches exist to deal with them. Each has its own set of tradeoffs, so we’ll discuss some of them in the upcoming sections.

Adding support for Removals: the Set-pair Approach

A first approach to deal with removals is the Set-pair technique. In a nutshell, instead of using a Set to represent the elements, we are going to use two: one for the additions and one for the removals. It might seem confusing at first, so let’s try to take it step by step.

Let’s start with an empty set, which will be represented internally by two add-only sets:

elements = {}
removals = {}

Then, we add elements a and b:

elements = {a, b}
removals = {}

If we now want to remove b, we could try deleting it directly from the elements set, but we would then experience the same flakiness problem saw previously. Instead, we are going to add the b element to the removals set:

elements = {a, b}
removals = {b}

We can now define the content of the Set as:

All the elements in the elements Set that are not present in the removals Set.

We can implement this Set by elegantly composing two CRDTAddOnlySet together:

class CRDTSet {
    constructor() {
        this.elements = new CRDTAddOnlySet();
        this.removals = new CRDTAddOnlySet();
    }

    add(element) {
        this.elements.add(element);
    }

    has(element) {
        if (this.removals.has(element)) {
            return false;
        }

        return this.elements.has(element);
    }

    remove(element) {
        this.removals.add(element);
    }

    merge(otherSet) {
        this.elements.merge(otherSet.elements);
        this.removals.merge(otherSet.removals);
    }
}

const replicaA = new CRDTSet();
replicaA.add('a');
console.log(replicaA.has('a')); // true

const replicaB = new CRDTSet();
replicaB.merge(replicaA);

replicaA.remove('a');
console.log(replicaA.has('a')); // false

replicaA.merge(replicaB);
console.log(replicaA.has('a')); // false (still false, yey!)

As you can see, our new Set remembers the removed element a even after a synchronization!

Unfortunately, our current CRDTSet still has some problems:

1. What happens if a replica adds an element after removing it? With the current implementation, once an element has been removed it won’t be restorable.
2. Although we are logically removing elements, the size of our data structure keeps increasing over time. If we perform many removals, that would bloat our memory consumption significantly.

In the next chapter, we are going to answer these two questions and more, so stay tuned!

PS: All the code is available in this repository: https://github.com/federico-terzi/crdt-experiments